-
표면 밝기 등급 - Surface Brightness [일반]
-
조회 수: 7161, 2017-10-13 00:07:53(2017-04-15)
-
이번주 매수팔 스터디 시간에 함께 이야기하다 나온 질문 중 다음으로 답을 미뤘던 것이 하나 있었습니다.
"NSOG의 정보를 보면 표면밝기 등급(Surface Brightness; SB)의 값이 겉보기등급(Apparent Magnitude)보다 작은(밝은) 값으로 나와있는 경우가 있던데, 표면 밝기 등급이 안시등급보다 밝을 수가 있는건가?" 가 질문이었습니다. 천체의 전체 면적에 걸쳐 나오는 빛을 한 점에 모은 것으로 계산한 겉보기 등급보다 그 면적에 고르게 밝기가 펼쳐져 있다고 가정하고 단위 면적의 밝기를 계산한 표면 밝기가 더 밝을 수 없을 것 같다는 생각이었죠. 자료의 오류인지 정말 가능한 건지 알아보자는 얘기를 했었습니다.
집에 돌아와 NSOG의 내용을 확인해보고, 관련된 자료를 좀 뒤적여 봤습니다. (매수팔 스터디 후 뒤풀이 공부 하는 재미가 좀 있습니다 ㅎㅎ)
결론부터 말하면 '있다'입니다.
표면밝기의 정의는 단위 면적(1 arcsec2; 1초각의 제곱) 당 밝기등급입니다. 겉보기 등급과는 단위에서 차이가 있습니다. 겉보기 등급의 단위가 '등급' 이라면, 표면 밝기 등급의 단위는 굳이 쓰자면 '등급/arcsec2'가 됩니다. 어떤 천체의 밝기를 그 천체의 면적으로 나눈 값을 등급으로 표시하면 표면 밝기 등급으로 나타낼 수 있는데, 이 때 나누어주는 면적이 단위면적인 1 arcsec2보다 작으면 천체의 겉보기 등급보다 작은(밝은) 값의 표면 밝기 등급을 얻을 수 있겠습니다. 면적이 0.5이고 밝기가 50와트인 물체의 단위 면적당 밝기는 100와트라고 말해야하는 거니까요.
마치 야구에서 1이닝만 던져 1점 실점한 투수의 평균 자책점(9이닝 당 평균 자책점)이 9점인 것과 비슷하다고 할까요 ^^
수식으로도 알아봤습니다. (수식이 싫으신 분은 아래 빨간 색으로 쓴 수식부터 보시면 됩니다. 제 계산 과정이 틀렸을 수도 있고요 ㅎㅎ)
면적을 가진 천체의 겉보기 등급은 그 전체 면적에서 나오는 빛의 총합으로 그 등급을 나타냅니다. 그 천체가 점광원이라고 생각하였을 때의 밝기라고 생각하면 되며, 예를 들어 겉보기 등급 10등급의 은하가 전체 면적에 걸쳐 내는 밝기의 총합은 겉보기 등급 10등급의 별의 밝기와 같습니다.
천체의 등급은 5등급 차이가 밝기로는 100배 차이 나도록(1등급과 6등급의 밝기 차이가 100배) 정의되어 있습니다.
등급이 다른 두 천체의 겉보기 밝기와 겉보기 등급 사이 관계를 나타내는 수식으로 이 정의를 표현해 보면,
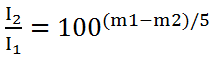
(천체 1, 2가 있다고 할 때, 두 천체의 겉보기 등급을 각각 m1, m2라 하고 겉보기 밝기를 각각 I1, I2라 하면)
위와 같이 쓸 수 있습니다.
위 식을 상용로그를 사용해 등급 차에 대해 다시 풀어 쓰면,
이 됩니다.
이 식을 표면밝기 등급을 구하는데 이용해보면,
(등급을 그냥 표면적으로 나눌 수는 없고 ^^; 전체 밝기를 표면적으로 나눈 값이 등급으로 하면 몇등급 정도에 해당하는지 위 식을 이용해 유추해볼 수 있겠습니다.)
m을 천체의 겉보기 등급, I를 천체의 겉보기 광도, S를 천체의 표면적(arcsec2단위), ms를 표면밝기 등급, Is를 단위 면적당 밝기(겉보기 밝기를 표면적으로 나눈 값; Is = I/S)으로 놓고 위 식에 대입해보면
이 되고, Is 대신 I/S를 대입하고 정리해보면
가 됩니다.
면적 S의 값이 1보다 큰 천체는 표면밝기 ms의 값이 겉보기 등급 m보다 큰(어두운) 값이 되지만, 1보다 작은 값을 가지면 logS가 음수가 되고 ms가 m보다 작은(밝은) 값이 됩니다. 예를 들어 0.5"×0.5" 크기를 가진 천체의 겉보기 등급이 12.0등급이라면 이 천체의 표면밝기 등급은 12.0 + 2.5log(0.5×0.5) = 12.0 - 1.5 = 10.5 등급이 됩니다. (log0.25 는 약 -0.6)
이 식이 표면밝기 등급을 구하는 정확한 식이 아닐수는 있지만 근사값을 구하는데는 사용될 수 있을 것 같습니다. (사실 구해놓고 여러 자료를 찾아봤는데, 표면밝기를 구할 때 위 식을 쓴 자료도 있었고, 더 복잡한 식을 쓴 자료도 봤습니다. 정확한 수식은 천문학자들께 패스 ㅎ)
정리하면
또 괜히 이야기를 길게 썼습니다만 겉보기 크기가 아주 작은 천체는 실제 보이는 것과 달리 작은(밝은) 표면밝기 등급 값을 가질 수 있다는 것을 알았고, 보통은 관측의 난이도를 판단할 때 표면 밝기를 참고하는 것이 좋지만, 1 제곱초(1 arcsec2)보다 작은 천체의 경우는 겉보기등급(안시등급) 값을 참고하는 것이 표면밝기 등급을 참고하는 것보다 실제에 가깝겠다는 생각입니다.

댓글 4
-
김남희
2017.04.15 07:53
-
최윤호
2017.04.15 22:49
단위 면적의 기준 때문에 그런거군요. 단위 면적의 기준을 더 낮추면 혼선이 없을 것 같습니다.
항상 분석 자료 감사합니다. -
김민회
2017.06.28 20:27
논문을 보는 것 같습니다. 잘 이해 못하게 수식과 함수를 써 대니까요.ㅎ 이해가 가도록 서너번 더 읽겠습니다. 참, 숨은 보물이세요. 님은! -
수정되어야 할 내용이 있어 http://www.nightflight.or.kr/xe/203789 에 추가 글을 올렸습니다.
| 번호 | 분류 | 제목 | 이름 | 조회 | 등록일 |
|---|---|---|---|---|---|
| 86 | 일반 | 류혁 | 5007 | 2019-01-19 | |
| 85 | 일반 | 최윤호 | 4245 | 2018-08-31 | |
| 84 | 일반 | 김승희 | 5392 | 2018-03-21 | |
| 83 | 일반 |
개기일식 관측 성공 비법
+11
| 조강욱 | 5581 | 2017-11-06 |
| 82 | 일반 | 박상구 | 5291 | 2017-10-26 | |
| 81 | 일반 | 박상구 | 5880 | 2017-10-12 | |
| 80 | 일반 | 김민회 | 30374 | 2017-06-15 | |
| 79 | 일반 |
Abell 스터디자료
+4
| 박진우 | 6369 | 2017-06-12 |
| ⇒ | 일반 | 박상구 | 7161 | 2017-04-15 | |
| 77 | 일반 | 박상구 | 5320 | 2017-03-16 |

나도 ebs 들어가서 수학,물리 좀 들어봐야겠네요.~~